|
仕事だけでなく個人的なことも含めて, |
|
第17回 日本酒部活動報告
ナンモリ通信 2014.05.02 号 writer:高田 |
|---|
|
今年の1月に入部した高田と申します。
しばらくすると,料理が次々と運ばれてきます。
前菜に始まり,サラダ,ピザ,パスタ…と,かなりのボリュームがあります。
私は赤ワインと一緒にいただきましたが,最高でした。
GWが近いこともあって,休みの過ごし方について話が盛り上がります。
次回の活動は,5月の中ごろになると思われます。 |
|
第16回 日本酒部活動報告
ナンモリ通信 2014.03.31 号 writer:越田 |
|---|
|
桜の花が咲き始め,屋外で一献傾けるのにもよい頃合いとなってきました。
テレビの右に少し見えているのがビールのサーバーです。
料理をいただきつつお酒を飲んでいきます。
お酒に合う料理が次々と出てきます。
お酒が進み,皆さん思い思いに楽しみました。
今回もおいしいお酒を楽しめました。
|
|
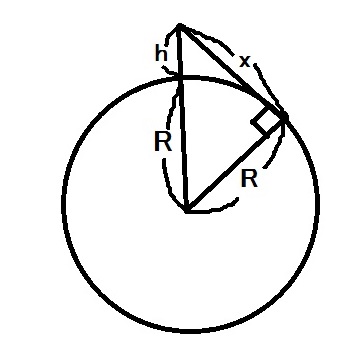
3ケタの数字と地平線
ナンモリ通信 2014.02.28 号 writer:別所 |
|---|
|
寒い日が続きますが,皆様いかがお過ごしですか。
具体的なxの値は,R=6400kmなので,h=2m(人の身長くらい)だと,約5kmです! |